Binary Search Algorithm, Definition, Code

By | January 4, 2024

Varun Saharawat is a seasoned professional in the fields of SEO and content writing. With a profound knowledge of the intricate aspects of these disciplines, Varun has established himself as a valuable asset in the world of digital marketing and online content creation.

Full Bio > Follow

binary search algorithm

A Binary Search Algorithm is an efficient algorithm for finding an item from a sorted list of items. The algorithm works by repeatedly dividing the list into half portions, which can contain the item to be searched until we narrow down the possible location to just one. In the end, if the element is present in the list, its index is returned. In this article, we will learn about the Binary search algorithm. 

What is a Binary Search Algorithm?

The Binary Search Algorithm is an efficient searching algorithm that uses the divide and conquer method to search for an element in a sorted array or list. It is one of the most popular searching algorithms. It is more efficient than linear search algorithms.

Under this algorithm, we compare the target value with the middle element and decide which half will most probably contain the target value. The algorithm then shifts to that part of the list. It keeps on dividing itself until the start and end pointers coincide. The time complexity of the binary search algorithm is in logarithmic time, O(logn), where n is the number of elements in the array. It works faster than a linear searching algorithm, as here, we do not have to traverse the whole array.

Also Read: Python vs Java: Which is Best for Machine learning algorithm

Important Points For Binary Search Algorithm

Some major important highlights of the binary search algorithm must be kept in mind.

  • The Binary search algorithm works only on a sorted array or list.
  • It works on a divide-and-conquer approach.
  • The time complexity of the binary search algorithm is logarithmic.
  • Binary search is faster and more efficient than linear search algorithm.
  • It is efficient for large datasets.

Binary Search Algorithm 

The algorithm for binary search is given in the table below.

Binary Search Algorithm
binary_Search( a, lower_bound, upper_bound, target)

Step 1: set start = lower_bound, end = upper_bound, pos = – 1  

Step 2: repeat steps 3 and 4 while start <=end  

Step 3: set mid = (start + end)/2  or start+(end-start)/2

Step 4: if a[mid] = target 

set pos = mid  

print pos  

go to step 6 

else if a[mid] > target

set end = mid – 1

else  

set start = mid + 1  

[end of if]  

[end of loop]  

Step 5: if pos = -1  

print “Not Present”  

[end of if]  

Step 6: exit  

Working on Binary Search Algorithm 

The binary search algorithm is a searching algorithm that works on the divide and conquer principle. It searches the target element in a sorted array.

Consider a sorted array, arr[ ]= { 2,6,11,16,22,34,39}. Now, let us search for an element X= 2. We will use a binary search algorithm to find the index of the element in the array.

  • Step 1: First we need to calculate the mid value of the array by using the formula given below.

                                    mid = (low+high)/2

  • Step 2: At the beginning, keep low = 0 and high = size-1. 
  • Step 3: Now, let us calculate the value of mid. Hence, the element at index 3 is the mid-value.

                                 mid = (0+6)/2 =  3.

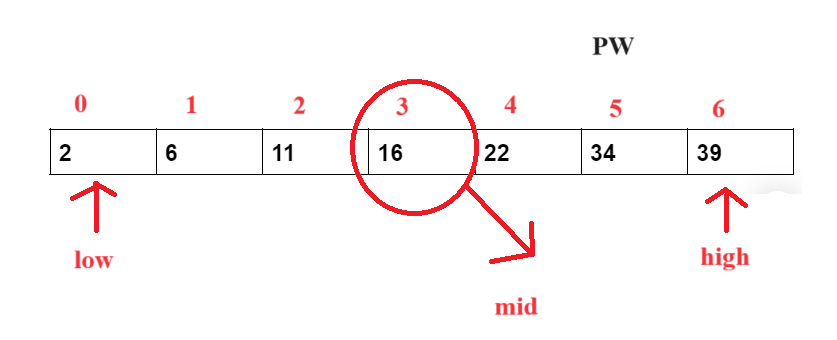
binary search algorithm

  • Step 4: Now, we will check whether the target element is greater or less than the arr[mid]. Here, our target element is lesser than the arr[mid], i,e. 2<16. Hence, now we will take our high value to mid-1.

                                 high = mid-1

  • Now, our array will reduce to the following. Now calculate the mid value again.

                                            mid= (0+2)/2=1

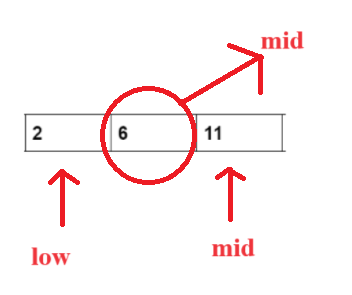
binary search algorithm

  • Now, we again check whether the target element is greater than or less than the arr [mid], i.e., 2<6. Hence, we again reduce the size of our array and take high to mid-1.
  • Now, our low and high both point to the same index. Now, calculate the mid value. We find that the arr[mid]== X, i.e., 2==2. Now, we will return the index of the element.

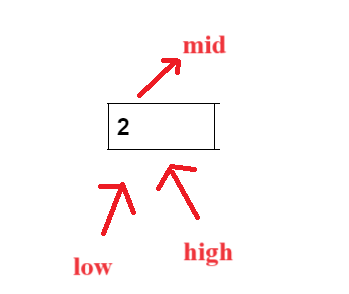
binary search algorithm

  • If the element is not present in the array, then the low and high will cross each other then return -1.

Also Read: Full Form of OOPS

Time and Space Complexity of Binary Search Algorithm

The binary search algorithm works in logarithmic time complexity with constant space. Check the binary search algorithm’s best, average and worst time complexity below.

Time Complexity of Binary Search Algorithm
Case Time Complexity
Best Case O(1)
Average Case O(logN)
Worst Case O(logN)
  • The best-case complexity happens when our target element is found in the first iteration, i,e. It is the first middle element. The best time complexity of the binary search algorithm is O(1).
  • The average time complexity of the binary search algorithm is O(logn).
  • The worst time complexity occurs when our target element is the last. We keep dividing until the last element is left, our target element. The worst time complexity of the binary search algorithm is O(logn).

The space complexity of the binary search algorithm is O(1). It requires a constant space, and no additional space is required for this algorithm.

Space Complexity of Binary Search Algorithm
O(1)

Difference Between Linear Search Algorithm and Binary Search Algorithm

The two most popular search algorithms are linear and binary search algorithms. Let us highlight some of their major differences below.

Difference Between Linear Search and Binary Search Algorithm
The Linear Search algorithm works by traversing the complete list one by one to search the target element. The Binary Search Algorithm is an efficient algorithm for finding an item from a sorted list of items
It does not require the list element to be sorted. It requires the elements to be in sorted order.
The time complexity of the linear search algorithm is O(N), where N is the number of elements in the array. The time complexity of a binary search algorithm is O(logN), where N is the number of elements in the list.
It only works with the divide-and-conquer approach. It works on the divide and conquer approach.
It is simple but inefficient for large datasets. It is suitable for large datasets.

Implementation of Binary Searching Algorithm In C++

Check the C++ code for implementing the binary search algorithm.

Binary Search Algorithm using C++
  1. #include <iostream>  
  1. using namespace std;  
  2. int binarySearch(int a[], int low, int high, int X)   
  1. {    
  2.     int mid;    
  1.     if(high >= low)     
  2.     {  
  3.         mid = (low+ high)/2;
  4.     
  5. /* if the target value is present in the mid */ 
  1.         if(a[mid] == X)    
  2.         {                 
  3.             return mid+1;    
  4.         }    
  5.    /* if the item to be searched is smaller than middle, then it can only be in the left subarray */  
  1.         else if(a[mid] < X)     
  2.         {  
  3.             return binarySearch(a, mid+1, high, X);    
  4.         }    
  6.  /* if the item to be searched is greater than middle, then it can only be in the right subarray */      
  1.     else     
  2.         {  
  3.             return binarySearch(a, low, mid-1, X);    
  4.         }         
  5.     }    
  6.     return -1;     
  7. }   

Implementing Binary Search Algorithm With Java 

Check the Java code to implement the binary search algorithm in the table below.

Binary Search Algorithm Using Java
class BinarySearch { 

  1.     static int binarySearch(int a[], int low, int high, int X)   
  1.     {    
  2.         int mid;    
  3.         if(high>= low)     
  4.         {  
  5.             mid = (low+ high)/2;    
  7.             if(a[mid] == X)    
  8.             {    
  9.                 return mid+1; 

 /* if the item to be searched is present in the middle  

           */  

  1.     }    

/* if the item to be searched is smaller than the middle, then it can only  

  1. be in the left subarray */  
  1.             else if (a[mid] < X)     
  2.             {  
  3.                 return binarySearch(a, mid+1, end, val);    
  4.             }  
  5.   

 /* if the item to be searched is greater than middle, then it can only be  

  1. in right subarray */  
  2.             else    
  3.             {  
  4.                 return binarySearch(a, low, mid-1, X);    
  5.             }    
  6.         }    
  7.         return -1;    
  8.     }   

Binary Search Algorithm FAQs

What is a binary search algorithm?

The Binary Search Algorithm is an efficient algorithm for finding an item from a sorted list of items. The algorithm works by repeatedly dividing the list into half portions, which can contain the item to be searched until we narrow down the possible location to just one.

Is binary search the most efficient algorithm?

Yes, a binary search algorithm is a more efficient algorithm than a linear search algorithm. It is considered one of the best search algorithms as it works on the divide-and-conquer approach.

Why is it called binary search?

The binary search algorithm works by dividing the complete array into more than one halves and then shifting the array to the probable part where we can find our target element. Hence, it is called binary search algorithm.

What are the four steps of a binary search algorithm?

The complete four steps of the binary search algorithm are:

Set the search space by setting up the starting and end pointer. The start pointer points to the first index, and the endpoints to the last index.
Now calculate the mid-element.
Shift the pointers to the favourable part of the array.
If an element is found, return the index. If not found, return -1.

Must Read

Telegram Group Join Now
WhatsApp Channel Join Now
YouTube Channel Subscribe
right adv
right adv
right adv
right adv
right adv
right adv

Related Articles

Scroll to Top
bottom banner bottom banner mobile
close
close
counselling
Want to Enrol in PW Skills Courses
Connect with our experts to get a free counselling & get all your doubt cleared.